이것저것 공부기록
6. 완전탐색(백트랙킹, 상태트리와 CUT EDGE)-DFS 기초 본문
0. 재귀함수와 스택
재귀함수: 자기 자신을 호출하는 함수, 재귀함수는 스택으로 구현된다.
반복문을 대체할 수 있는 것이 재귀함수.
사용자에게 n이라는 수를 입력받으면, 1부터 n까지 출력해주는 프로그램을 만들어보자.
def DFS(x):
if x > 0: # x에 0이 들어오면 종료
print(x, end = ' ')
DFS(x-1)
if __name__ == "__main__":
n = int(input())
DFS(n)DFS(x) 함수는 재귀함수이고, 위 코드를 실행한 결과는 다음과 같다.

그러나 우리는 1부터 출력하기로 했으므로 코드를 다음과 같이 수정한다.
def DFS(x):
if x > 0: # x에 0이 들어오면 종료
DFS(x-1)
print(x, end = ' ')
if __name__ == "__main__":
n = int(input())
DFS(n)
바뀐 것은 print문의 위치 뿐인데, 원하던 결과가 나왔다.
이렇게 결과가 나올 수 있는 것은 재귀함수가 스택을 이용하여 구현되어있기 때문이다.
(함수가 호출되는 순서대로 스택에 쌓임)

위 상황은 DFS 함수에 매개변수로 0이 들어가서 종료되고 리턴된 뒤, DFS(1) 함수가 1을 출력하고 리턴하는 상황이다.
이처럼 스택에 차곡차곡 쌓였다가 마지막 리턴 주소로 돌아가기 때문에 1 2 3 오름차순으로 출력될 수 있는 것이다.
1. 재귀함수를 이용한 이진수 출력
사실 나는 이진수의 특성? 10진수에서 2진수로 어떻게 바뀌는지를 이해하고 응용해야 된다고 생각했는데, 그런 류의 문제는 아니었던 것 같다.
def DFS(x):
if x == 0: # 종료 조건 필수
return
else:
DFS(x//2)
print(x%2, end = '')
if __name__ == "__main__":
n = int(input())
DFS(n)
2. 이진트리 순회(깊이우선탐색)
DFS(Depth-First Search)
gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html
[알고리즘] 깊이 우선 탐색(DFS)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
* 있으면 계속 파고들어가고(깊게), 더 내려갈 수 없으면 이 전으로 뒤로 돌아가서(back) 다른 방향으로 또 내려간다.
• 전위순회: 부모→왼쪽 자식→오른쪽 자식
• 중위순회: 왼쪽 자식→부모→오른쪽 자식
• 후위순회: 왼쪽 자식→오른쪽 자식→부모
DFS 초보자는 DFS 함수의 구조를 일단 if-else문으로 생각하자.
## 전위순회 방식 ##
def DFS(v):
if v > 7:
return
else:
print(v, end = ' ') # 부모 노드를 가장 먼저 출력
DFS(v*2) # 왼쪽 노드 호출
DFS(v*2+1) # 오른쪽 노드 호출
if __name__ == "__main__":
DFS(1)## 중위순회 방식 ##
def DFS(v):
if v > 7:
return
else:
DFS(v*2) # 왼쪽 노드 호출
print(v, end = ' ') # 왼쪽을 모두 처리하고 부모를 출력.
DFS(v*2+1) # 오른쪽 노드 호출
if __name__ == "__main__":
DFS(1)## 후위순회 방식 ## 병합 정렬이 이 방식을 사용.
def DFS(v):
if v > 7:
return
else:
DFS(v*2) # 왼쪽 노드 호출
DFS(v*2+1) # 오른쪽 노드 호출
print(v, end = ' ') # 왼쪽과 오른쪽을 전부 출력한 후에 그 부모를 출력.
if __name__ == "__main__":
DFS(1)3. 부분집합 구하기(DFS)
부분집합의 개수는 n^2개 (공집합 포함)이므로 공집합을 제외한 부분집합의 개수는 (n^2 - 1)개이다. (별로 중요하지는 않음)
** DFS 문제 대부분은 전순위 방식인데, 상태 트리를 어떻게 구성하느냐가 중요하다.
def DFS(v):
if v == n+1:
for i in range(1, n+1):
if ch[i] == 1:
print(i, end = '')
print()
else:
ch[v] = 1 # 원소를 부분집합에 포함시킴
DFS(v+1)
ch[v] = 0 # 원소를 부분집합에 포함시키지 않음
DFS(v+1)
if __name__ == "__main__":
n = int(input())
ch = [0]*(n+1) # 사용하느냐 마느냐 체크할 변수
DFS(1)
이 트리처럼 원소를 부분집합에 포함하느냐(O), 마느냐(X)를 ch 배열을 통해 조정한다고 생각하면 된다.
4. 합이 같은 부분집합(DFS: 아마존 인터뷰)
문제를 읽자마자 3번 문제처럼 원소를 포함 하느냐 마느냐로 부분집합의 합을 따지면 되지 않을까?하는 생각이 들었다.
그렇게 생각하고 짠 코드는 다음과 같다.
def DFS(v):
global switch
if switch: return
if v == n+1:
sum1 = 0
sum2 = 0
for i in range(1, n+1):
if ch[i] == 1:
sum1 += a[i]
else:
sum2 += a[i]
if sum1 == sum2:
print("YES")
switch = 1
else:
ch[v] = 1 # 원소를 부분집합에 포함시킴
DFS(v+1)
ch[v] = 0 # 원소를 부분집합에 포함시키지 않음
DFS(v+1)
if __name__ == "__main__":
n = int(input())
a = list(map(int, input().split()))
a.insert(0, 0)
ch = [0]*(n+1) # 사용하느냐 마느냐 체크할 변수
switch = 0
DFS(1)
if switch == 0:
print("NO")코딩테스트에서는 sys 라이브러리 사용이 금지되어 있기도 해서, switch라는 글로벌 변수를 이용해 조건의 참과 거짓 여부를 가리도록 해주었다.
** 리스트는 메인 함수에서 초기화하고 지역 함수에서 바로 사용이 가능했는데, switch 변수는 사용이 불가능했다. (그래서 자꾸 안돼서 빡침) 해결 방법은 함수에서 global 변수로 선언해주는 것.
** 다음 강의 영상을 보니까, global로 선언해주지 않았을 때는 지역변수로써 switch라는 변수가 새롭게 만들어졌기 때문에 메인함수의 변수를 변경하지 못했던 것 같다. (=, 할당 연산자가 사용되면 지역변수로 생성됨)
def DFS(L, sum): # L(level)은 리스트 a를 참조할 인덱스 번호, sum은 내가 만든 부분집합의 합
if L == n:
if sum == (total - sum):
print("YES")
sys.exit(0) # 함수가 종료되는 것이 아니라, 프로그램을 아예 종료하는 명령
else:
DFS(L+1, sum+a[L])
DFS(L+1, sum)
if __name__ == "__main__":
n = int(input())
a = list(map(int, input().split()))
total = sum(a)
DFS(0, 0)
print("NO")강사님의 첫 번째 코드이다. 어떤 부분집합의 합을 sum이라고 하면, 내가 선택하지 않은 나머지 원소들의 합은 (전체 집합의 합 - 부분집합의 합) 이라는 점을 이용했다. 그리고 DFS 함수에 매개변수 2개를 넘겨줌으로써 리스트에 접근하는 것이 용이해졌다.
✔ 매개변수로 sum 값을 함께 넘겨줌으로써 ch 리스트로 관리할 필요가 없어졌다. 즉, 2번 문제에서 ch[i] = 1 : sum+a[L], ch[i] = 0 : sum 으로 대응된다고 생각하면 될 것 같다.
def DFS(L, sum):
if sum > total//2:
return
if L == n:
if sum == (total - sum):
print("YES")
sys.exit(0) # 함수가 종료되는 것이 아니라, 프로그램을 아예 종료하는 명령
else:
DFS(L+1, sum+a[L])
DFS(L+1, sum)
if __name__ == "__main__":
n = int(input())
a = list(map(int, input().split()))
total = sum(a)
if total % 2 == 0: # 내가 추가한 부분
DFS(0, 0)
print("NO")강사님이 시간복잡도를 줄이기 위한 방법으로 소개하신 코드이다.
결국 한 부분집합과 부분집합을 제외한 나머지 원소들의 합이 같으려면 sum // 2보다는 작아야 한다고 하셨다. 그래서 DFS 함수의 첫 행에 if문이 추가되었다.
그런데 이 말을 듣고 나니까 든 생각이, 어차피 문제 조건에서 자연수가 주어진다고 했으므로 합이 홀수일 때는 절대 조건에 맞는 부분집합이 존재할 수 없지 않은가? 그래서 total이 짝수일 때만 DFS 함수를 실행하도록 했다.
전역변수와 지역변수
• 메인함수에서 선언되면 전역변수
• 전역변수는 모든 함수에서 접근 가능 → 다른 함수에서 전역변수를 사용하려면 global 선언 필수
** 리스트는 왜 global 선언을 하지 않아도 전역변수로써 사용 가능한가?
def DFS():
a[0] = 7
print(a)
if __name__ == "__main__":
a = [1, 2, 3]
DFS()
print(a)
→ DFS() 함수에서 리스트를 새로 생성한 것이 아니기 때문. 참조 리스트 정도로 생각하면 된다.
a[0] = 7을 만났을 때, a라는 리스트가 로컬 함수에 존재하지 않기 때문에 전역변수를 참조하는 것이다.
def DFS():
a = [7, 8]
print(a)
if __name__ == "__main__":
a = [1, 2, 3]
DFS()
print(a)
이렇게 해야 로컬 리스트인 a가 새로 생성되는 것이다.
def DFS():
a = a + [4]
print(a)
if __name__ == "__main__":
a = [1, 2, 3]
DFS()
print(a)
위같은 경우는 에러를 발생시킨다. 이 에러를 발생시키지 않으려면 역시 global 선언을 해주면 된다.
def DFS():
global a
a = a + [4]
print(a)
if __name__ == "__main__":
a = [1, 2, 3]
DFS()
print(a)
5. 바둑이 승차(DFS)
보자마자 익숙한 듯한 느낌이 들었는데, 그리디 알고리즘으로도 풀 수 있는 거 아닐까 생각했다. (다 더해놓고 가벼운 무게부터 빼기) 그런데 만약 가벼운 순서대로 A, B, C 가 있고 트럭에 태울 수 있는 최대 무게가 w라고 했을 때 B + C > w 이지만 A + C < w 일 수 있으므로 잘못된 접근이다.
모르겠어서 강의를 듣다가, 초반에 부분집합 문제랑 똑같다고 하시는 걸 듣고 떠오른 게 있다. 부분집합의 합을 구해서 최대값을 계속 갱신하면 되지 않을까? 4번 문제랑 유사하다.
def DFS(L, sum, tsum):
global result
if sum + (total - tsum) < result: # cut edge
return
if sum > c:
return
if L == n:
if sum > result:
result = sum
else:
DFS(L+1, sum+a[L], tsum+a[L]) # 다음 원소를 부분집합에 포함 O
DFS(L+1, sum, tsum+a[L]) # 다음 원소를 부분집합에 포함 X
if __name__ == "__main__":
c, n = map(int, input().split())
a = []
for _ in range(n):
a.append(int(input()))
result = -2147000000
total = sum(a)
DFS(0, 0, 0)
print(result)변수 tsum은 레벨 L까지 거쳐온 값의 합이다. sum에 넣고 말고와 관계 없이 무조건 다 더한 값.
이걸 왜 구하냐면, (total - tsum) 값은 결국 앞으로 처리(더하거나 말거나)해야 할 값들의 합이 되는데, 거기에 지금까지 선택한 값들의 sum을 더했을 때 result보다 작다면 다음 과정을 굳이 할 필요가 없기 때문이다. 그래서 바로 return.
cut edge(시간 단축을 위한 것..?)을 위한 것인 것 같다.
DFS 응용은 언제쯤 할 수 있을까.. 이런 게 알고리즘이란 것인가.. 하..
6. 중복순열 구하기(DFS)
DFS 문제는 상태트리를 어떻게 구성하느냐가 중요. 탐색은 DFS로 하면 되니까.
def DFS(L):
global cnt
if L == m:
for x in res:
print(x, end = ' ')
print()
cnt += 1
else:
for i in range(1, n+1):
res[L] = i
DFS(L+1)
if __name__ == "__main__":
n, m = map(int, input().split())
res = [0]*m # m개의 숫자를 뽑아 저장할 리스트
cnt = 0
DFS(0)
print(cnt)강사님 설명 듣고 내가 짠 코드! 맞았다. 근데 이걸 어떻게 생각해내...
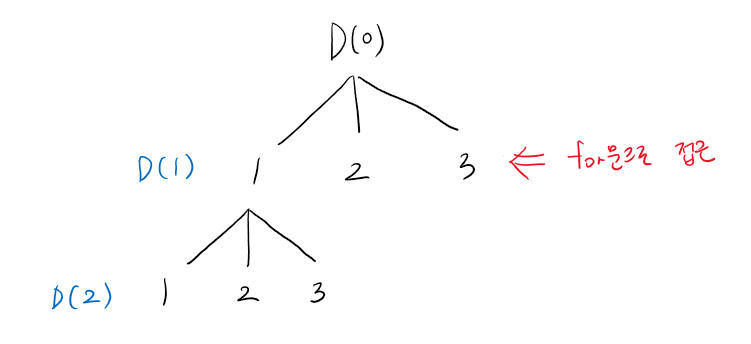
7. 동전 교환 - Cut Edge Tech
if __name__ == "__main__":
n = int(input())
kind = list(map(int, input().split()))
kind.sort()
m = int(input())
cnt = 0
while m != 0:
if m >= kind[-1]:
m -= kind[-1]
cnt += 1
else:
kind.pop()
print(cnt)일단 보자마자 짠 코드이다. 가장 금액이 큰 동전부터 쓰는 것이 동전을 최소로 쓸 수 있는 방법이 아닐까 생각했는데, 3번 예제를 보니 꼭 그런 것만은 아니었다. (그리디 알고리즘 X)
* 앞서 풀었던 중복순열 문제와 같이 상태 트리를 구성하면 된다.
* 동전교환 문제는 DFS 방식이 아니라 다이나믹 프로그래밍 방식-냅색 알고리즘으로 푸는 게 더 효율적이다. (섹션 8에 냅색으로 같은 문제 다룸. 여기서는 중복순열을 응용해보기 위해 N 제한을 작게 둬서 사용한 것이라고 하심)
def DFS(L, sum): # L이 동전의 사용 개수가 됨
global res, m
if sum > m: # sum > m이면 더 깊이 탐색할 필요 X, 바로 리턴
return
if L > res: # L이 res보다 커지면 바로 리턴. 더 탐색할 필요 없음.
return
if sum == m:
if L < res:
res = L
else:
for i in range(n):
DFS(L+1, sum + a[i])
if __name__ == "__main__":
n = int(input()) # 동전 종류의 개수
a = list(map(int, input().split())) # 동전의 종류
m = int(input())
res = 2147000000
a.sort(reverse=True)
# 전위순회방식으로 탐색할 것이기 때문에 오름차순으로 정렬되어 있으면 첫 경우에 시간이 너무 오래 걸리기 때문.
DFS(0, 0)
print(res)강사님 강의를 조금 듣다가 완성한 코드. 100점이 나오기는 했다. 처음에는 DFS 함수의 앞 부분에 있는 두 개의 if문을 아예 생각하지도 못했었다. 그래서 실행 시간이 굉장히 길었던 것 같은데, 탐색을 마무리할 조건만 생각하는 게 아니라 더 이상 탐색하지 않아도 되는 조건까지 생각해보아야 할 것 같다.
전체적인 풀이 방식은 위 중복순열 문제와 같다. 상태트리 그려보기!
8. 순열 구하기
중복순열 문제랑 엄청 비슷한데, 중복을 어떻게 피할 건지가 문제이다. → ch 리스트 활용
def DFS(L):
global cnt
if L == m:
for x in res:
print(x, end = ' ')
print()
cnt += 1
else:
for i in range(1, n+1):
if ch[i] == 0:
ch[i] = 1
res[L] = i
DFS(L+1) # 이 행을 중심으로 위쪽과 아래쪽은 대칭구조
ch[i] = 0 # back한 후의 행동
if __name__ == "__main__":
n, m = map(int, input().split())
cnt = 0
ch = [0] * (n+1)
res = [0] * m
DFS(0)
print(cnt)뭐지..? 강의 들으면서 대충 이거겠지~ 했는데 맞아버렸네.. ㅋㅋ
특히 else문 부분이 이게 맞나 싶었는데, 강의에서처럼 예제 하나를 가지고 그냥 차례대로 따라가기만 해도 맞는 코드를 짤 수 있는 것 같으니 앞으로 그렇게 해보도록 하자. 괜히 복잡하게 생각할수록 더 어렵다.
9. 수열 추측하기(순열, 파스칼 응용)
뭔가 획기적인 아이디어가 있는 줄 알았는데, 그냥 만들어질 수 있는 수열을 모두 확인해보아야 한다.
1~4로 만들 수 있는 수열의 개수 = 4! = 4*3*2*1 = 24개
그러나 n =10이라고 가정하면, 1~10으로 만들 수 있는 수열의 개수는 엄청나다. 이걸 다 하나하나 확인해보려면 당연히 Time Limit에 걸리겠지? → 모두 계산해보지 않아도 수학적으로 확인할 수 있다.
(그냥 규칙 찾기였네...)

이처럼 맨 왼쪽과 맨 오른쪽 숫자는 딱 1번씩만 더해지고, 2와 3은 3번씩 더해진 꼴이다.
이항계수
n = 3) 1 2 1
n = 4) 1 3 3 1
n = 5) 1 4 6 4 1 = 4C0 4C1 4C2 4C3 4C4
...

def DFS(L, sum):
if L == n and sum == f:
for x in p:
print(x, end = ' ')
sys.exit(0) # 이 프로그램을 종료
else:
for i in range(1, n+1):
if ch[i] == 0:
ch[i] = 1
p[L] = i
DFS(L+1, sum + p[L]*b[L])
ch[i] = 0
if __name__ == "__main__":
n, f = map(int, input().split())
p = [0]*n
b = [1]*n # 이항계수 리스트
ch = [0]*(n+1) # 순열 만들 때 중복 방지하기 위한 체크리스트
for i in range(1, n): # 이항계수 리스트 초기화
b[i] = b[i-1]*(n-i) // i
DFS(0, 0)
** itertools (순열이나 조합을 알아서 구해줌) 라이브러리를 이용해서 풀 수도 있음. 그러나 코딩테스트에서 라이브러리 사용을 막아놓을 수 있기 때문에 라이브러리에 너무 많이 의존하지는 말기. (강의 있음)
10. 조합 구하기(DFS)
이 문제를 응용해서 푸는 문제가 많으므로 꼭 잘 익혀두기!
+) 백준 N과 M 시리즈 문제들
def DFS(L, s):
global cnt
if L == m:
for x in res:
print(x, end = ' ')
print()
cnt += 1
else:
for i in range(s, n+1):
res[L] = i
DFS(L+1, i+1) # 중요, (i+1) - 가지를 뻗는다고 생각
if __name__ == "__main__":
n, m = map(int, input().split())
cnt = 0
res = [0]*m
DFS(0, 1)
print(cnt)강의에서처럼 상태트리를 생각하고는 있었는데, 변수를 제대로 활용하지 못했다..
주석 체크한 부분이 핵심!
중복을 없애는 코드 + (a, b)라 했을 때 b > a 라는 조건만 생각해주면 된다.
* 뒤의 조건만 생각해봐도 중복은 자연스레 없어짐.

11. 수들의 조합(DFS)
def DFS(L, s):
global cnt
if L == k:
sum = 0
for x in res:
sum += x
if sum % m == 0:
cnt += 1
else:
for i in range(s, n):
res[L] = a[i]
DFS(L+1, i+1)
if __name__ == "__main__":
n, k = map(int, input().split())
a = list(map(int, input().split()))
m = int(input())
res = [0]*k
cnt = 0
DFS(0, 0)
print(cnt)이 문제는 뭐.. 10번 조합 코드를 아주 살짝만 고쳐주면 된다. 가볍게 success! 근데 이것만 주면 풀 수 있을지는..ㅎㅎ 조합을 어떻게 뽑는지 그 기본 형태만 알고 있으면 풀 수 있는 문제인 듯 하다.
def DFS(L, s, sum):
global cnt
if L == k:
if sum % m == 0:
cnt += 1
else:
for i in range(s, n):
DFS(L+1, i+1, sum+a[i])
if __name__ == "__main__":
n, k = map(int, input().split())
a = list(map(int, input().split()))
m = int(input())
cnt = 0
DFS(0, 0, 0)
print(cnt)이 코드는 강사님 코드이다. 굳이 res 리스트로 값을 관리할 필요 없이, DFS 함수에 매개변수로 sum을 포함시켜줌으로써 코드를 더 간단하게 쓸 수 있다.
12. 인접행렬(가중치 방향그래프)
n, m = map(int, input().split())
res = [[0]*n for _ in range(n)]
for _ in range(m):
s, e, c = map(int, input().split())
res[s-1][e-1] = c
for i in range(n):
for j in range(n):
print(res[i][j], end = ' ')
print()
인접행렬이 뭔지, 그래프를 어떻게 행렬로 나타내는지 알아보는 문제였다.
이산수학 배울 때 배웠던거라 어렵지는 않았음.
다만, 이게 뭐지? 싶었던 건 res 리스트를 만들 때 였는데, 위처럼 코드를 짜면 괜찮은데
res = [[0]*n]*n
이렇게 짜면 결과가 이따구로 나온다... 아무래도 res 리스트가 2차원 리스트로 초기화된 게 아니라 여러 개의 리스트를 포함하는 뭐 대충 그런 걸로 만들어져서, 값이 한번에 모두 바뀌어버린다. 기억해둘 것.
** 나랑 똑같은 생각을 하고 질문하신 분이 계셨는데, 강사님께서
res = [[0]*n]*n 같이 생성하면 모양은 비슷하지만 동일한 1차원 리스트를 여러번 복사했을 뿐이라고 알고 계신다고 답변을 하셨다.
13. 경로 탐색(그래프 DFS)
내가 생각했던 방법은, 인접행렬을 초기화해두고 1부터 n까지 DFS로 탐색하며 행렬 값이 1이면 그 경로를 거쳐 가고, 아니면 back해서 찾는 방법이었다. 방법은 맞는 것 같은데 코드 짜는게 어렵다.😂
* 한 번 방문한 노드는 다시 방문할 수 없다. 원래 그래프 이론에서 "경로"의 정의는 방문한 노드는 재방문하지 않는다고 되어 있다. → 방문한 노드 체크 필요
def DFS(v): # vertex - 노드 번호
global cnt
if v == n: # 정점 n에 도달했을 때
cnt += 1
else:
for i in range(1, n+1): # i가 방문하려는 노드 번호
if res[v][i] == 1 and ch[i] == 0: # v 노드에서 i 노드로 갈 수 있는지, i 노드에 방문한 적이 없는지 확인
ch[i] = 1
DFS(i)
ch[i] = 0
if __name__ == "__main__":
n, m = map(int, input().split())
res = [[0]*(n+1) for _ in range(n+1)]
ch = [0]*(n+1)
for _ in range(m):
s, e = map(int, input().split())
res[s][e] = 1
cnt = 0
ch[1] = 1 # 1번 노드는 처음에 방문하므로
DFS(1)
print(cnt)
상태 트리를 그려가면서 깊이 들어가고 back하는 과정을 직접 해보는게 중요! 강의 들으면 이해는 다 되는데.. 복습할 땐 하나하나 내가 다 해보면서 코드를 이해해보자.
'Python Algorithm' 카테고리의 다른 글
| 7. 깊이, 넓이 우선탐색 활용 (0) | 2021.03.25 |
|---|---|
| 5. 자료구조(스택, 큐, 해쉬, 힙) (0) | 2021.03.06 |
| 4. 이분 탐색(결정 알고리즘)&그리디 알고리즘 (0) | 2021.01.06 |
| 3. 탐색&시뮬레이션(string, 1차원, 2차원 리스트 탐색) (0) | 2021.01.04 |
| 2. 코드 구현력 기르기 (0) | 2020.07.16 |

