이것저것 공부기록
알고리즘 기수스터디 - 하노이 탑 본문
하노이 탑이란, 하나의 축에 크기가 각기 다른 원반이 쌓여 있고, 제3의 축을 이용하여 작은 원반 위에 큰 원반이 놓여지지 않도록 하면서 한 번에 한 장씩 움직여 다른 축으로 원반의 이름을 이동시키는 퍼즐의 이름이다. (컴퓨터인터넷IT용어대사전)
<문제>
1. 첫번째 줄에 장대에 쌓을 원판의 개수(N)을 입력한다. (1<=N<=20)
2. 두 번째 줄에 몇 번(K)에 걸쳐 과정을 수행하는지 출력한다.
3. 3번째 줄부터 과정들을 출력한다. (A B 출력 - A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다.)
원반이 1개이면 1번만 이동시키면 되고,
원반이 2개이면 2번만 이동시키면 되고,
원반이 3개이면 7번을 이동시키면 된다.
귀납적 방법으로 원반의 개수에 따른 하노이 탑의 이동 횟수를 추론해보면
원반의 개수가 N일 때, 이동 횟수는 2^N-1회이다.
코드를 찾고 나서도 재귀함수의 흐름에 대해서 이해가 잘 되지 않았다.
그래서 원반의 개수를 비교적 작게 3개로 하여 직접 과정을 그려보며 그 흐름부터 이해해보고자 한다.

초기 상태이다. 이때 1번 장대에 있는 원반 3개를 2번 장대로 모두 옮길 것이다. 원반의 개수는 3이고, 빨간색 원반의 반지름을 3, 노란색 원반의 반지름을 2, 초록색 원반의 반지름을 1이라고 생각하겠다. (하노이 탑에서 작은 원반 위에 큰 원반이 올라가면 안되기 때문에)

먼저, 1번에 있던 가장 작은 원반(1)을 2로 옮긴다. 이때 3번 장대는 2번으로 모든 원반을 옮기기 위해 사용될 임시 장대이다.
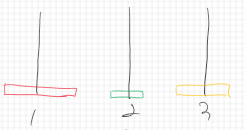
1번 장대에 있는 노란색 원반(2)를 3번 장대로 옮긴다.

2번 장대에 있는 초록색 원반(1)을 3번 장대로 옮긴다.
지금까지의 과정은 결국 2개의 원반, 즉 (n-1)개의 원반을 옮긴 것과 같다.
→ n개의 원반을 다 옮기는 과정 안에서 (n-1)개의 원반을 다 옮기는 과정이 포함되어있다.
(이 과정이 함수 내에서 또 그 함수를 호출하는, 재귀함수의 방식이라고 생각된다.)

1번 장대에 있던 빨간색 원반(3)을 2번 장대로 옮긴다.

3번 장대에 있던 초록색 원반(1)을 1번 장대로 옮긴다.

3번 장대에 있던 노란색 원반(2)을 2번 장대의 빨간색 원반 위로 옮긴다.

1번 장대에 있던 초록색 원반(1)을 2번 장대로 옮기면 모든 과정이 끝난다.
정리하면, 핵심은 아래와 같다.
1. 첫 번째 재귀에서는 맨 밑의 N번째 원반을 목적지로 옮기기 위해 위의 (N-1)개의 원반을 경유지로 옮긴다.
2. 그 다음 N번째 원반을 목적지로 옮긴다.
3. 경유지에 있는 (N-1)개의 원반을 목적지로 옮긴다.
(https://shoark7.github.io/programming/algorithm/tower-of-hanoi 참고)
이러한 과정을 코드로 구현하면 아래와 같다.
#include <iostream>
using namespace std;
void hanoi(int n, int start, int to, int via)
{
if (n == 1)
cout << start << " " << to << endl;
else
{
hanoi(n - 1, start, via, to); // (n-1)개의 원반을 경유지로 재귀적으로 모두 옮김
cout << start << " " << to << endl; // n번 원반을 목적지로 옮김
hanoi(n - 1, via, to, start); // 경유지에 있던 원반들을 목적지로 재귀적으로 모두 옮김
}
}
int main()
{
int N, K;
cin >> N; // 첫번째 장대에 쌓을 원판의 개수 입력
K = pow(2, N) - 1; // N개의 원판이 있을 경우 필요한 이동 횟수 => 2^N-1
cout << K << endl;
hanoi(N, 1, 2, 3);
return 0;
}
내가 위에서 그린 그림과 같은 결과가 출력된다.
? 실제 하노이의 탑을 할 경우에는 원판의 개수가 짝인지 홀인지에 따라 첫번째 원판의 이동을 달리 선택해야한다. 하지만 재귀호출의 경우에는 역으로 모든 경우를 탐색한 후 회귀를 하는 방식이기때문에 짝수인지 홀수인지에 관해서 신경쓸 필요가 없다 ?
--> 다른 분들의 설명도 보고 싶어 윤진님의 문서화 글 읽다가, 나도 같은 사이트를 보았던 것인지 이 부분에 대해서 의문점이 생겼었는데 그 부분을 빼먹었어서 추가함. 재귀함수를 설명하는 유튜브 영상(youtu.be/aPYE0anPZqI)에서 보니까 홀수인지 짝수인지에 따라 홀수이면 첫번째 원판을 목표 기둥에, 짝수이면 원판을 경유지 기둥에 ... 이런 식으로 달라지는 것 같았는데, 그렇다면 왜 실제 하노이의 탑을 할 경우에는 꼭 달리 선택해야 하는지 등 아직 완벽하게 이해하지 못한 부분들이 많은 것 같음.
'언어 > C++ 스터디' 카테고리의 다른 글
| WEEK_7 과제 1 참조 (0) | 2020.07.27 |
|---|---|
| WEEK_3 과제 1 포인터 (0) | 2020.05.22 |
| WEEK_2 과제2 별 찍기 시스템 (0) | 2020.05.17 |
| WEEK_1 과제3 C++ 기초 (0) | 2020.04.12 |



